How To Divide A Triangle Into 3 Equal Parts

How three medians meeting at centroid divides triangle area into 3 and 6 equal parts and properties of cevians

Centroid divides triangle area into 3 equal parts formed past the longer median segments at centroid and 6 equal parts by all half dozen median segments at centroid.

Too a point on a cevian divides a triangle area in the ratio of its segments at the signal.

Medians meeting at centroid create a rich prepare of relations involving fragmented areas and segmented lines including the sides of the triangle.

Contents are,

1. How each median divides triangle area into two equal parts.
2. How three medians segmented at centroid divides triangle surface area into vi equal parts.
3. How iii medians meeting at centroid divides triangle surface area into three equal parts by their longer segments.
4. Relation between areas of the triangles formed by the medians at centroid and a line parallel to a base and passing through the mid-points of the other 2 sides.
5. Expanse to cevian segment ratio concept: A triangle area is divided in the same ratio as the cevian segment ratio at a point that acts every bit the vertex of a second triangle.
6. Expanse of triangle from length of medians.

A median divides a triangle into 2 parts of equal surface area

In the following figure, AD is a median of $\triangle ABC$ bisecting the opposite side BC at D. The centroid is the signal G through which the other 2 medians, if drawn, would pass. AH is the distance of the triangle with BC as the base; and PAQ is a line parallel to base BC.

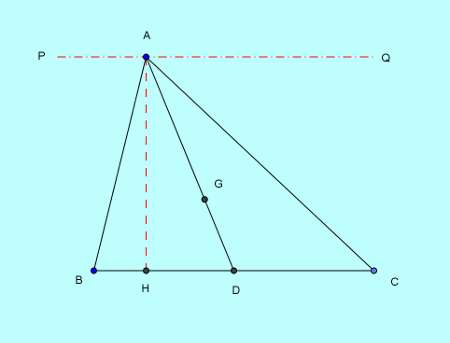
With base of operations BC and altitude AH the area of $\triangle ABC$ is,

$A=\frac{ane}{2}BC\times{AH}$.

As $BD=CD=\frac{one}{2}BC$, area of $\triangle ABD$ is,

$A_{ABD}=\frac{1}{2}BD\times{AH}=\frac{1}{iv}BC\times{AH}=\frac{1}{two}A$.

For $\triangle ADC$ also distance is same AH, like any triangle with base BC and vertex lying on line PAQ parallel to it. So area of $\triangle ADC$ is,

$A_{ADC}=\frac{1}{2}DC\times{AH}=\frac{ane}{4}BC\times{AH}=\frac{1}{two}A$.

Thus the median Advertizing divides the area of the triangle into two equal parts.

Before we next evidence you how three medians separate the area of a triangle into six equal parts, we volition generalize the first upshot into the powerful concept of Area to base of operations sectionalization ratio , and prove its mechanism.

Area to base partitioning ratio concept

The post-obit figure represents the problem solution.

In $\triangle ABC$, as line segment Advertizing from vertex A to base of operations BC divides BC in the ratio of, $CD:BD=x:y$, the ratio of areas of $\triangle ACD$ and $\triangle ABD$ will also be $x:y$. To formally state this of import general result,

A line segment from a vertex of a triangle to the opposite side, which is the base of operations, divides the base of operations and the triangle expanse in the aforementioned ratio.

Proof of area to base segmentation ratio concept

In $\triangle ABC$, line segment Advertisement divides the base BC at D so that,

$CD:BD=x:y$.

Equally both the triangles, $\triangle ACD$ and $\triangle ABD$ have same altitude AP which is too the altitude of parent $\triangle ABC$,

$\text{Area of }\triangle ABD=A_{ABD}=\frac{1}{two}BD\times{AP}$.

Similarly,

$\text{Area of }\triangle ACD=A_{ACD}=\frac{1}{ii}CD\times{AP}$.

Taking the ratio of the latter to the former,

$A_{ACD}:A_{ABD}=CD:BD=10:y$.

The result is really simple but general.

A special case is when AD is the median and $CD=BD$. In this case and then, the median divides the triangle into two parts of equal areas.

Equally another example, if $BD=2CD$,

$A_{ABD}=2A_{ACD}$.

Nosotros will use this last issue to explain how the iii medians divide a triangle into six regions of equal area.

All three medians together split a triangle into vi equal parts, proof

The following figure will assistance explain the mechanism of this human relationship. AD, Be and CF are the iii medians dividing the $\triangle ABC$ into six office triangles meeting signal of which is the centroid Grand. AP is the perpendicular to median BE and is the altitude of all three triangles $\triangle ABG$, $\triangle AEG$ and $\triangle ABE$.

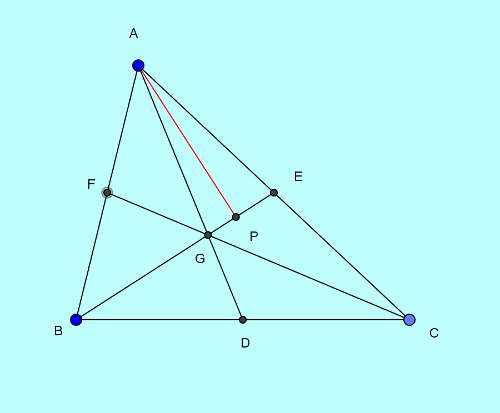
The medians dissever the triangle into half-dozen non-overlapping triangular regions with vertices meeting at centroid G. These half dozen triangles really consist of three pairs of equal triangles formed past the sectionalisation of three triangles formed from the centroid and three pairs of vertices, by the office of median from vertex G to the base. For case, areas of 1 such equal expanse pair of triangles concord the relation,

$A_{BGD}=A_{CGD}$.

Our objective is to evidence expanse of one adjacent pair of the three pairs of triangles as equal. For example nosotros volition show,

$A_{AFG}=A_{AEG}$.

$\triangle ABE$ is divided into two triangles $\triangle ABG$ and $\triangle AEG$ by the median department $AG$ incident on base BE at G.

As Be is a median, past the median section ratio at centroid concept, it is divided into two sections BG and EG with a ratio, $BG:EG=2:1$ .

So by the expanse to base of operations division ratio concept,

$A_{ABG}=2A_{AEG}$.

Again, in $\triangle ABG$,

$A_{ABG}=2A_{AFG}$.

Thus,

$A_{AEG}=A_{AFG}$, that is, a pair of next triangles are equal in area.

This makes areas of all six triangles with coincident vertices at G equal.

3 vertex to centroid line segments carve up a triangle into iii equal parts

By this concept, G being the centroid, in figure below GA, GB and GC divide the triangle into 3 equal parts.

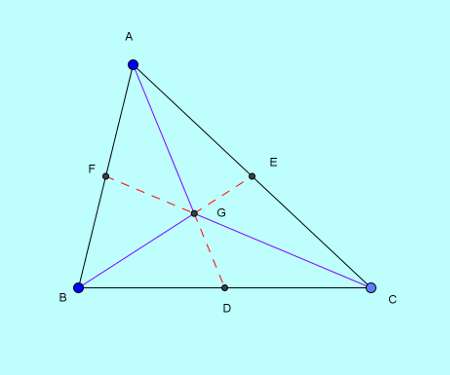
This can easily exist ended by adding upwardly side by side equal pairs of half dozen equal triangles created by the three medians as in the previous section.

Earlier nosotros proceed to the adjacent sections we demand to explain the frequently used Triangle similarity rich concept.

Triangle similarity rich concept, the mechanism

The following effigy will aid explanation of the concept.

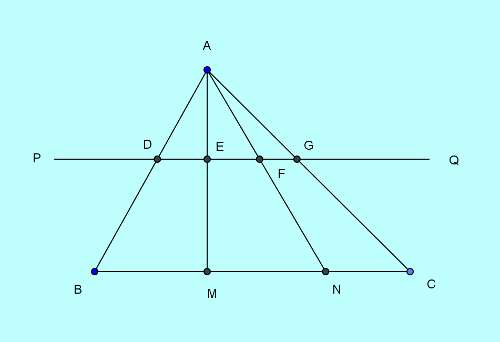
Nosotros formally land the triangle similarity rich concept equally,

Ratio of all pairs of corresponding sides of corresponding pairs of triangles formed by a straight line parallel to the base will be equal.

Alternatively this result leads to,

A straight line parallel to the base of operations of a triangle volition split all straight line sections dropped from the vertex to the base in equal ratio.

This powerful rich concept is used oft in both forms.

To exist specific, with respect to the figure above, the line $PQ||BC$, the base, cuts across four lines $AB$, $AM$, $AN$ and $AC$ dropped from vertext A to the base BC at the points D, E, F and G respectively in equal ratio. That is to say,

$Advertizement:BD=AE:EM=AF:FN=AG:GC$.

This is the second form of the rich concept and it follows from the broader first form of the definition of the concept.

Primary form of the triangle similarity rich concept

The line PQ||BC forms six pairs of corresponding triangles past cut across the four lines dropped from the vertex to the base of operations,

$\triangle ADE$ and $\triangle ABM$,

$\triangle AEF$ and $\triangle AMN$,

$\triangle AFG$ and $\triangle ANC$,

$\triangle ADF$ and $\triangle ABN$,

$\triangle AEG$ and $\triangle AMC$, and finally,

$\triangle ADG$ and $\triangle ABC$.

In each such pair of triangles, the ratio of the respective sides will be equal, so that ratio of all pairs of respective sides volition be equal.

This amounts partially to,

$\displaystyle\frac{Advertizement}{AB}=\frac{AE}{AM}=\frac{AF}{AN}=\frac{AG}{Air conditioning}=\frac{DG}{BC}$.

There will be more such equal ratios.

This happens primarily considering, say in the pair of triangles, $\triangle ADG$ and $\triangle ABC$,

• the angle at the vertex $\angle A$ is common, and
• the rest of the two pairs of angles, $\bending ADG=\angle ABC$, and $\angle AGD =\bending ACB$, as each of AB and AC intersects a pair of parallel lines DG and BC.

The 3 pairs of respective angles beingness equal, the $\triangle ADG$ and $\triangle ABC$ are similar so that ratio of all three pairs of corresponding sides become equal.

The same mechanism works in every pair of corresponding triangles.

Information technology is footling to show that this result leads to the second grade of definition of this of import rich concept.

We need to explain 1 more rich concept, the surface area to cevian segment ratio , before taking up the next sections.

A cevian is,

A line from a vertex reaching or crossing the opposite side of a triangle.

Surface area to cevian segment ratio concept, proof

The following figure volition assist the definition and proof of concept.

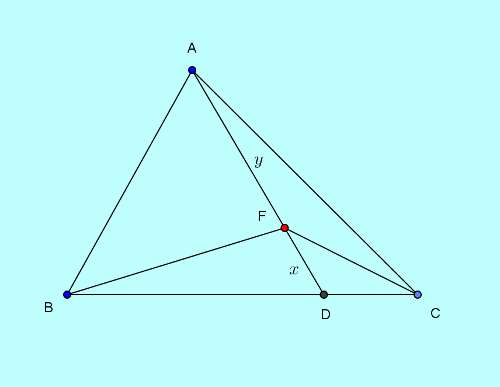
A cevian is divers as,

A line from a vertex reaching or crossing the contrary side of a triangle.

In effigy above AD is such a cevian. Special cases of cevians are, the median and the distance of the triangle.

Surface area to cevian segment ratio concept formally states,

Whatever bespeak on a cevian dividing the line into a ratio of $x:y$ will besides divide the whole area of the triangle into ii regions in the same ratio by acting as the vertex of 2nd triangle inside the principal triangle.

Alternately,

Ratio of the ii line sections fabricated by a point on a cevian will be same as the ratio of the two areas formed by the bespeak as a vertex of a triangle with base same as the original triangle.

Specifically with respect to the effigy,

$AF:FD=\text{Area of region }ABFCA:\text{Surface area of }\triangle BFC$.

Here point F divides the cevian Advertising into two sections FD and AF at a ratio of $x:y$.

Information technology follows from this result,

$FD:AD=A_{AFD}:A_{ABC}=x:(x+y)$.

We go this issue just by fraction inversion, addition of 1 and so inversion back.

Permit united states come across why this concept works.

In $\triangle ABD$ with AD as base, applying expanse to base of operations partitioning ratio concept ,

$A_{DBF}:A_{ABF}=FD:FA=x:y$.

Similarly in $\triangle ACD$ with Ad equally base, and applying the same concept we get,

$A_{DCF}:A_{ACF}=FD:FA=10:y$.

Then past ratio concepts,

$A_{BFC}:A_{ABFC}=x:y$,

Or, $A_{BFC}:A_{ABC}=x:(x+y)$.

Special example of centroid every bit the cevian point on a median, the cevian in this case

As a special case, if F is the centroid, AD is a median so that F divides the median in a ratio,

$FD:AF=1:2$, and so in this special case,

$A_{BFC}:A_{ABC}=one:3$.

In other words, the expanse of the $\triangle BFC$ will exist 1-3rd of the primary $\triangle ABC$.

With these rich concepts in place nosotros are now ready to go ahead in dealing with the balance of the concepts elegantly.

Additional useful relations between the areas of the triangles formed by the medians at the centroid

We will use the following figure to explain the concept in this section. Specifically nosotros volition see how the area of the triangles $\triangle GFP$, $\triangle GEP$ or $\triangle BGC$ are related to each other and to the surface area of the primary $\triangle ABC$.

In this section we will explore what are the ratios of the areas of the triangles, $\triangle GFP$, $\triangle GFE$ and $\triangle BGC$ with respect to the area of the parent triangle.

Area of $\triangle GFP$ with respec to area of $\triangle GFE$

Equally median Advertizing is the line from vertex to the last triangle base BC, passing through the bases of triangles, $\triangle AFE$ and $\triangle Historic period$, where these 2 have a mutual base FE, the median Advertising bisects FE as well at P. Nosotros conclude this upshot past applying the Triangle similarity rich concept.

Then,

$FP=EP$.

Thus GP divides the $\triangle GFE$ in 2 equal parts. We conclude this from the concept of a median bisecting the area of a triangle.

This consequence says then,

$A_{GFP}=\frac{1}{2}A_{GFE}$.

Area of $\triangle GFE$ with respect to area of $\triangle ABC$

To solve this trouble we volition decide the extent of GP.

Past triangle similarity rich concept ,

$AP=DP=DG+PG$.

Adding PG to the equation,

$AP+PG=AG=DG+2PG$.

Again past median department ratio at centroid concept ,

$AG=2DG=DG+2PG$.

And so,

$DG=2PG$, which we suspected to be true, but at present we know.

Equally $DG=\frac{1}{3}Advert$,

$PG=\frac{i}{6}Advertizement$, where $Advertisement$ is the median.

Flipping $\triangle GFP$ vertically with its vertex moved along the median

When nosotros do this, we form the rectangle GEHF with its diagonals bisected at P, and its area bisected by mutual base of operations FE.

Also,

$PH=PG=\frac{ane}{half-dozen}AD=\frac{1}{3}AP$.

By area to cevian segment ratio concept then,

$A_{GFE}=A_{FHE}=\frac{i}{3}A_{AFE}=2A_{GFP}$,

Too,

$A_{AFE}=\frac{one}{iv}A_{ABC}$, as both base and altitude of the smaller triangle are half of those of the larger triangle.

Relating the areas of all these triangles,

$A_{GFP}=\frac{1}{2}A_{GFE}=\frac{1}{6}A_{AFE}=\frac{ane}{24}A_{ABC}=\frac{1}{8}A_{BGC}$.

The terminal event we go fro an earlier result of,

$A_{BGC}=\frac{1}{3}A_{ABC}$, equally GD is 1-third of Advertising.

Annotation that we have not used the distance or the base lengths. We could avoid this because of symmetric human relationship betwixt the median and the bases and hence the areas through the use of the powerful rich concepts.

Area of triangle from lengths of its medians, proof

The figure below volition aid the caption.

As usual, AD, BE and CF are the three medians of $\triangle ABC$ intersecting at centroid Thousand.

The values, $AD=m_1$, $Exist=m_2$ and $CF=m_3$ are given. We are to derive the area of the $\triangle ABC$.

Every bit nosotros know, given 3 sides of a triangle equally a, b and c, its semi-perimeter,

$south=\frac{1}{ii}(a+b+c)$, and the surface area,

$A=\sqrt{s(s-a)(s-b)(due south-c)}$.

We need and then to construct a triangle with three sides as the medians, derive relation betwixt the surface area of triangle of medians to the area of the original triangle and then get the area of the original triangle past deriving surface area of triangle of medians by using semi-perimeter concept.

Structure of triangle of medians

To construct the triangle of medians, starting time we have kept the side of median AD fixed, and translated the side of median BE in direction parallel to BC through the altitude BD to reach the position DQ. This parallel translation has resulted in, $Exist||DQ$ and $BE=DQ$ every bit well as, $EQ||BD||BC$ and $EQ=BD=DC$. This has formed the second side of the triangle of medians.

To form the 3rd side, the third median CF has been translated in management parallel to AB to AQ, so that, $CF||AQ$ and $CF=AQ$ as well as, $CQ||AF||AB||DE$ and $CQ=AF=FB=DE$.

In resulting parallelogram DEQC, the 2 diagonals bifurcate each other, so that, $ER=CR$ and $DR=QR$, then that AR is the median of $\triangle ADQ$ that is fabricated up of medians ot the original $\triangle ABC$.

Thus AR divides the area of $\triangle ADQ$ into ii equal parts each of which, say, is $x$.

AS $AE=EC=2ER$, $AR=AE+ER=3ER$, that is,

$ER=\frac{1}{3}AR$, giving

$A_{DER}=A_{DCR}=\frac{1}{3}A_{ADR}=z$, say.

Now we will use the following figure simplified from the above figure to put forth the final piece of reasoning.

We have removed the medians Be and CF every bit a cleanup measure.

Let united states of america denote,

Surface area of $\triangle ABD=A_{ABD}=y$,

Surface area of $\triangle ADR=A_{ADR}=ten$, and

Area of $\triangle DCR=A_{DCR}=z$.

And expanse of $\triangle ABC$ is, $A_{ABC}=2y$, and area of $\triangle ADQ$ is, $A_{ADQ}=A_m=2x$.

Now,

$A_{ACD}=y=x+z=10+\frac{1}{3}10=\frac{4}{3}x$.

So,

$A_{ABC}=\frac{4}{3}A_m$.

In other words, the area of any triangle is four-thirds of the expanse of the triangle formed from its medians.

Every bit we know how to find the surface area of a triangle from its given side lengths, it is a simple step more to observe the area of the $\triangle ABC$ from the given length of its medians.

Lastly we will only skim through the question of finding the area of an equilateral triangle in terms of its sides or medians.

Area of an equilateral triangle from its sides and medians

The following effigy volition help the caption.

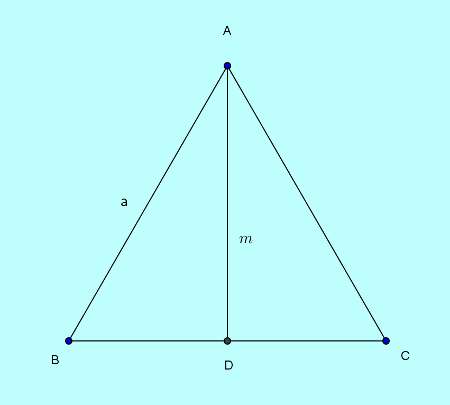
Equally median AD of equilateral $\triangle ABC$ of side length $a$ is perpendicular to contrary side BC bisecting information technology, the expanse of the triangle is,

$A_{ABC}=\frac{1}{2}BC\times{Advert}$.

Past the use of Pythagorean theorem we have,

$Advertisement=m=\sqrt{a^2-\left(\frac{a}{2}\right)^2}=\sqrt{\frac{3}{4}a^two}=\frac{\sqrt{iii}}{2}a$.

So,

$A_{ABC}=\frac{\sqrt{3}}{4}a^2=\frac{1}{\sqrt{three}}1000^2$, where $a$ is the side length of the equilateral $\triangle ABC$ and $m$ is the length of all its 3 medians.

Note: Existence USERS of knowledge for solving problems the best manner possible, we need to know the mechanism backside a concept in as clear terms as possible. The clarity of understanding of a concept goes a long way in increasing our belief on the concept and consequently our ability to utilise the concept when information technology is really needed.

---

Guided assistance on Geometry in Suresolv

To get the best results out of the extensive range of articles of tutorials, questions and solutions on Geometry in Suresolv, follow the guide,

Suresolv Geometry Reading and Practice Guide for SSC CHSL, SSC CGL, SSC CGL Tier II and Other Competitive exams.

The guide list of articles includes ALL articles on Geometry and relevant topics in Suresolv and is up-to-appointment.

---

←   →

Source: https://suresolv.com/basic-maths/basic-and-rich-geometry-concepts-part-6-proof-triangle-area-medians

Share this post